Évaluation des expressions arithmétiques sur une PRAM CREW

A.LEGRAND

Y.ROBERT

Novembre 3, 2005

Idées générales

Le sujet de ce devoir concerne l'évaluation d'une expression arithmétique $(+,-,\times,/)$ de longueur $n$ en temps $O(\log n)$ avec $O\left(\frac{n}{\log n}\right)$ processeurs sur une PRAM CREW. L'algorithme proposé est donc à la fois optimal en temps (regarder l'évaluation de $\sum_{i=1}^{2^m} x_i$) et en travail (puisque le travail global est de l'ordre de $n$). La première partie consiste à construire un arbre d'évaluation de l'expression arithmétique en temps $O(\log n)$ avec $O\left(\frac{n}{\log n}\right)$ processeurs et la seconde partie porte sur l'évaluation de cet arbre en temps $O(\log n)$ avec $O(n)$ processeurs (l'algorithme optimal étant trop long pour ce devoir) en utilisant des techniques de type saut de pointeurs. Contrairement à ce qu'on pourrait imaginer, le principe n'est pas de construire un arbre très densepour utiliser le schéma de réduction appliqué à une somme par exemple. L'idée est de construire un arbre qui se prête bien à une évaluation pseudo-formelle .

En effet, dans le cas général, il n'est pas facile de construire un arbre d'évaluation équilibré pour une expression arithmétique. Regardons par exemple l'évaluation d'un polynôme par le schéma de Horner: \begin{equation*} a_1 + x \times ( a_2 + x \times ( a_3 + x \times (a_4 +x ))) \end{equation*} Les arbres naturels correspondant au schéma de Horner et à la forme développée sont présentés dans la figure 1.

Figure: Arbres d'évaluation du polynôme.
\includegraphics[width=.9\linewidth]{horneval.fig}
L'évaluation avec la forme développée conduit à un arbre mieux équilibré mais elle introduit des calculs redondants et ne permet donc pas une évaluation beaucoup plus rapide. Dans la figure 2, nous présentons brièvement le schéma d'évaluation que nous allons utiliser. L'idée est d'associer à chaque n\oeud (i.e. chaque opérateur) de l'arbre une fonction et d'utiliser une forme de saut de pointeur (afin d'obtenir le temps en $O(\log n)$) pour évaluer l'expression.

Figure: Arbre d'évaluation symbolique du polynôme.
\includegraphics[width=.9\linewidth]{hornevsymb2.fig}

Construction de l'arbre d'évaluation


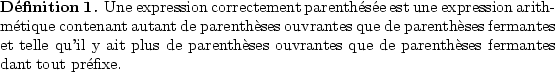
\begin{definition} Une expression correctement parenthésée est une expression ... ...èses ouvrantes que de parenthèses fermantes dant tout préfixe. \end{definition}


\begin{definition} Une expression simple est soit une variable entourée de pare... ...ité et où les $E_i$ sont elles mêmes des expressions simples. \end{definition}

\begin{definition}[La fonction match] Pour une expression correctement parenthé... ...e parenthèse ouvrante la penthèse fermante qui lui correspond. \end{definition}


\begin{Question} % latex2html id marker 61Écrire un algorithme qui transforme... ...caractère est remplace par au plus cinq caractères). \end{Reponse}\end{Question}

On considère maintenant une chaîne constituée uniquement de parenthèses (de longueur $2^m$ avec $m \vert 2^m$) obtenue par la suppression dans une expression simple de tous les autres caractères. On va montrer comment calculer la fonction match sur cette séquence de parenthèses.
\begin{definition} On définit l'opérateur de réduction $\mathcal{R}$ sur une p... ...ire quelconque de deux parenthèses successives est sans effet. \end{definition}


\begin{Question} Quelle est la forme d'une séquence réduite de parenthèses dans... ...}(^{l+j-k}\text{ si } j \geqslant k.\end{displaymath}\end{Reponse}\end{Question}


\begin{Question} Donner un algorithme parallèle pour construire un construire e... ...(\log n)$ avec $O(\frac{n}{\log n})$ processeurs. \end{Reponse}\end{Question}


\begin{Question} % latex2html id marker 177En déduire un algorithme séquentie... ...ion en temps $O(\log n)$ avec $O(n)$ processeurs. \end{Reponse}\end{Question}


\begin{Question} Montrer comment construire la fonction match pour toutes les ... ...ement $O\left(\frac{n}{\log n}\right)$ processeurs. \end{Reponse}\end{Question}

On est maintenant en mesure de proposer un algorithme pour construire l'arbre d'évaluation d'une formule simple. On rappelle que l'arbre d'évaluation correspondant à la formule simple

\begin{displaymath}((E_1) op_1 (E_2) \ldots op_{k-1} (E_k))\end{displaymath}

est indiqué à la figure 3.
Figure: Arbre d'évaluation correspondant à une expression simple.
\includegraphics[width=.7\linewidth]{arbexpsimple.fig}


\begin{Question} % latex2html id marker 252Proposer un algorithme qui constru... ...avec $O\left(\frac{n}{\log n}\right)$ processeurs. \end{Reponse}\end{Question}

Nous avons donc montré qu'il est possible de construire l'arbre d'évaluation d'une expression quelconque correctement parenthésée de longueur $n$ en temps $O(\log n)$ avec $O\left(\frac{n}{\log n}\right)$ processeurs.

Dans les questions suivantes, nous allons montrer comment évaluer l'expression en temps $O(\log n)$ avec $O(n)$ processeurs. Il est possible de réaliser cette évaluation en temps $O(\log n)$ avec $O\left(\frac{n}{\log n}\right)$ processeurs mais cela sort du cadre de ce devoir.

Évaluation de l'expression

Le principe de l'évaluation est le suivant. À chaque n\oeud $v$ de l'arbre d'évaluation, on va associer un n\oeud $cond(v)$. Au départ, pour tout n\oeud $v$ on pose $cond(v)=v$. Un n\oeud est dit marqué si on sait évaluer la valeur de l'expression du sous arbre enraciné en ce n\oeud. Dès qu'un des fils d'un n\oeud est marqué, on dit que le n\oeud est actif. À tout moment, si un n\oeud est actif, la connaissance de la valeur de $cond(v)$ doit être suffisante au calcul de la valeur de $v$ . Pour cela, on associe à chaque n\oeud actif une fonction de la forme $f(x)=\frac{ax+b}{cx+d}$, où $x$ représente la valeur de $cond(v)$. Pour obtenir une évaluation rapide de l'expression, l'idée est de faire du saut de pointeur sur $cond(v)$, ce qui nécessite de composer les fonctions associées au n\oeud.


\begin{Question} % latex2html id marker 289Montrer qu'il est possible de calc... ... exécutées en temps $O(1)$ avec $O(n)$ processeurs. \end{Reponse}\end{Question}

On définit une étape de l'algorithme d'évaluation de la fonction par la séquence (Marquer,Activer,Sauter,Sauter). Dans la suite, on va montrer qu'après $\log n$ étapes, tous les n\oeuds de l'arbre d'évaluation sont marqués, et donc en particulier que la racine contient la valeur de l'expression. On aura donc ainsi produit un algorithme qui évalue une expression quelconque en temps $O(\log n)$ avec $O(n)$ processeurs, puisque chaque étape est atomique avec $O(n)$ processeurs.


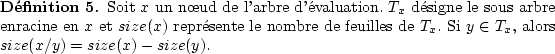
\begin{definition} Soit $x$ un n{\oe }ud de l'arbre d'évaluation. $T_x$ désig... ...s de $T_x$. Si $y \in T_x$, alors $size(x/y)=size(x)-size(y)$. \end{definition}
Pour démontrer la correction de l'algorithme, on a utiliser les deux invariants suivants
\begin{definition}[$(I1)_k$] Après $k$ étapes de l'algorithme, si $size(x) \leqslant 2^k$ alors le n{\oe }ud $x$ est marqué. \end{definition}

\begin{definition}[$(I2)_k$] Soit $x$ un n{\oe }ud de l'arbre. Après $k$ étap... ...t marqué, \item soit $cond(x)$ est une feuille. \end{itemize}\end{definition}


\begin{Question} Montrer $(I1)_{k}$ en utilisant $(I1)_{k-1}$ et $(I2)_{k-1}$... ...^k$, alors $x$ est marqué a la fin de l'étape $k$. \end{Reponse}\end{Question}


\begin{Question} % latex2html id marker 351Montrer $(I2)_{k}$ en utilisant $... ... a la dernière discussion.} \end{center} \end{figure}\end{Reponse}\end{Question}

Réponses aux exercices


Arnaud Legrand
2005-11-03