MIPS architecture

Memory organization
Processor organization
    Registers
     Instruction Set
Basic assembly language
Load and store
Arithmetic Operations
Input and Output System Calls
Function Calls and The Stack
Recursion
Floating Point Operations
Other Architectures

Memory organization

The purpose of memory is to store groups of bits, and deliver them (to the processor for loading into registers) upon demand. Most present-day computers store information in multiples of 8 bits, called a byte (or octet). Most also assign a numeric address to each byte. This is convenient because characters can be stored in bytes.
Memory addresses are 32-bit numbers, ranging from 0x00000000 to 0xFFFFFFFF. This is a large amount of memory, most computers do not have actual memory for all of this "address space."
Memory can hold both program instructions and data. One function of the operating system is to assign blocks of
memory for the instructions and data of each process (running program). Another thing a good operating system does is to allow many processes to run concurrently on the computer.

The SPIM simulator always assigns your program to these fixed, even numbered locations, for your convenience:

    0x00400000 - Text segment - program instructions
    0x10000000 - Data segment
    0x7FFFFFFF, and decreasing addresses - Stack segment

A word generally means the number of bits that can be transferred at one time on the data bus, and stored in a register. In the case of MIPS, a word is 32 bits, that is, 4 bytes.
Words are always stored in consecutive bytes, starting with an address that is divisible by 4. Caution: other processors, other definitions.
Some people refer to 16 bits as a word, to others it may mean 64 bits.
 

Storage order of words

How should one store a word (say, a register holding a number) in 4 bytes? There are two equally valid schemes: starting with the lowest numbered byte,

    Little Endian: Store the little end of the number (least significant bits) first, or
    Big Endian: Store the big end of the number first.

    (These terms come from Gulliver's Travels by Jonathan Swift, in which two parties are at war over whether hard-boiled eggs should be opened at the little end or the big end of the egg.)

MIPS is little-endian. One result of this is that character data appear to be stored "backwards" within words. Here is a representation of part of memory, storing the characters "Help" (0x706c6548) and then the number 32766  (0x00007ffe).
 
 

Processor organization

What a processor does, its function, can be completely described in terms of its registers, where it stores information, and what it does in executing each instruction. in the MIPS, all registers hold 32 bits.
 

Registers

The program counter (PC) always holds the address of the next instruction. Normally it is incremented every time an instruction is executed. This controls the flow of the program.

There are 32 general purpose registers, numbered 0..31. In assembly language, they also have symbolic names, which are shown in the register window of the SPIM simulator. These names suggest conventions for use of the registers. Registers may be referred to by name or number in assembly language, for instance, register 4 can be referred to as $4 or $a0, and is usually used for an argument to a procedure.

The first and last registers are special:

    $0 is a constant 0, and cannot be changed
    $31 stores the return address from a procedure (function) call. It is named $ra.

The conventions for usage we will adhere to are (a compiler for a high-level language may or may not adhere to these):
 
 

$1($at)	Assembler temporary. We will avoidusing it.
$v0 - $v1	- values returned by a function
$a0 - $a3	- arguments to a function (Pascal terminologyis: parameters to a procedure)
$t0 - $t9	- temporary use. Use freely but if youcall a procedure that procedure may change it.
$s0 - $s7	- saved by procedures. When you are writinga procedure; you must save and restore previous values.

 

Instruction set

Instructions can be grouped into the following catagories. The rest of the course covers the operations performed by the instructions, and how to use them in writing programs. Here I will just give an example of each type of instruction.
 

Load and Store : Load data from memory into a register, or store register contents in memory

    examples:      lw   $t0, num1    #load word in num1 into $t0
                          sw  $t0, num2    #store word in $t0 into num2, ie. num2 := num1
                          li   $v0, 4          #load immediate value (constant) 4 into $v0

Operations: Arithmetic and Logic : perform the operation on data in 2 registers, store the result in a 3rd register

    example:     add $t0, $t3, $t4     # $t0 := $t3 + $t4

Jump and branch : alter the PC to control flow of the program, producing the effects of IF statements and loops

There are also floating point instructions and registers, for real numbers. We will probably not get to these in this course.

Basic assembly language instructions

    load and store

    Arithmetic

    System calls

In this course we will be dealing with instructions on 3 different, relatively low, levels. Starting from the lowest (found left to right in the SPIM text segment window) they are:
 

  1.binary machine instructions (shown in hexadecimal)
  2.symbolic actual machine instructions. Registers shown numerically ($31)
  3.assembly language (nicer) instructions, the ones you write in a source file, registers can be referred to symbolically ($ra)

The correspondance is usually 1:1, however, since RISC is a Reduced instruction set, some normal and useful assembly language instructions can be coded as one or two other, less intuitive, instructions, so the assembler provides a limited translation service. In this section, I will only describe the nice instructions at level 3.
 
 
 

Load and store instructions

These instructions are used to move data between memory and the processor. There are always 2 operands, a register and an address. Addresses can take several forms, as we shall see, the simplest is the label of a data item.

In this example, a word (32 bits) is moved from Num1 to Num2, and a copy is left in register $t0:

        lw    $t0, Num1    # load word,  $t0 := Num1
        sw    $t0, Num2    # store word, Num2 := $t0

Note the order of the operands, the register is always first. The direction of movement is opposite.

There are similar instructions to load and store bytes (8 bits), half-words (16 bits), and double-words (64 bits)
 

Load immediate (constant)

There are also 2 instructions that load a constant, which is incorporated into the instruction itself (immediate):

    load immediate:    li  Rdest, Imm        # example:  li  $v0, 4
    load address:      la  Rdest, label      # example:  la  $a0, prompt_message

Since a label represents a fixed memory address after assembly, la is actually a special case of load immediate.

Note the difference between lw and la: If Num1 is at location [0x10001000] and contains 0xfffffffe (-2), then

    la   $a0, Num1   loads 0x10001000, while
    lw  $a0, Num1   loads 0xfffffffe
 
 
 

Arithmetic

Arithmetic is done in registers. There are 3 operands to an arithmetic operation:

  1.destination register
  2.Source 1 register
  3.Source 2 register or constant

The compact way of writing this pattern is:    add   Rdest, Rsrc1, Src2
The following code calculates the expression (x + 5 - y) * 35 / 3

                 lw    $t0, x             #load x from memory
           lw    $t1, y             #load y from memory
           add   $t0, $t0, 5        # x + 5
           sub   $t0, $t0, $t1      # x + 5 - y
           mul   $t0, $t0, 35       #(x + 5 - y)*35
           div   $t0, $t0, 3        #(x + 5 - y)*35/3
 

Arithmetic overflow, signed numbers

add, sub, mulo, & div check for overflow of signed numbers, an incorrect result, in which the sign bit is improperly altered. (mul doesn't do any checking). Usually we want to work with signed numbers. The processor generates an exception, "arithmetic overflow," and stops the program. This is preferable to generating incorrect results, as is usually the case with older processors, which generate a "flag" which programmers typically ignore.
 

Unsigned numbers

Sometimes we want to work with unsigned numbers. In this case overflow checking is unwanted. Generally we append a u to the operation code to express our intent. The unsigned operation codes are:

      addu,  subu,  mulou,   divu

This also applies to the short load instructions, lb and lh. They normally fill the unused part of the register with the sign bit of the short data. If we want to guarantee that the high part of the register is filled with 0's, we can use lbu & lhu instead. For example, we generally think of a character as an unsigned value.
 
 
 

Input and Output - System calls

Controlling the hardware responsible for input and output is a difficult and specialized job, and beyond the scope of this course. All computers have an operating system that provides many services for input/output anyway. The SPIM simulator provides 10 basic services. The ones we will be using right now are given here.

The others are for floating point (real) numbers. The call code always goes in $v0, and the system is called with syscall.
 
 

#    PROGRAM TO ADD TWO NUMBERS
#    Text segment
#               (all programs start with the next 3 lines)
        .text           #directive identifying the start of instructions
        .globl  __start

__start:

# -------------  print prompt on "console" --------------------
        la      $a0, prompt     # address of prompt goes in
        li      $v0, 4          # service code for print string
        syscall

# -------------  read in the integer --------------------------
        li      $v0, 5          # service code
        syscall
        sw      $v0, Num1       # store what was entered
# -------------- read another
        li      $v0, 5          # service code
        syscall
        sw      $v0, Num2       # store what was entered

# ------ Perfrom the addition, $a0 := Num1 + Num2
        lw      $t0, Num1
        add     $a0, $t0, $v0

# ------ print the sum, it is in $a0
        li      $v0, 1          # print integer service call
        syscall

# ------ print a final string identifying the result, and ending with a new line
        la      $a0, final
        li      $v0, 4
        syscall

        li      $v0, 10         # exit program service
        syscall

#------------------------------------------------------------------
#       Data segment
#------------------------------------------------------------------
        .data
Num1:   .word   0
Num2:   .word   0
prompt: .ascii  "Please type 2 integers, end each with the "
        .asciiz "Enter key:\n"
final:  .asciiz " is the sum.\n"

#------ end of file  ADDNUMS.ASM
 

Control structures

    Assembly language instructions for control of execution
    IF constructs
    Loops

So far we have seen how to move data between memory and processor registers, and how to do arithmetic in the registers. All are programs have been linear, a list of instructions carried out from start to exit. In this chapter we look at the assembly language instructions that alter the control flow of a program, and then at how these can be used to implement the high-level language constructs of if, while, & for.

The order of program execution is determined by the PC (program counter). It can be altered by changing the PC. This can be done by jump and branch instructions. Jump is just the notorious go to that has been supressed from high level languages. Branch instructions are so named because they offer an alternative, to branch or not. A "flow chart" of a program "branches" where there is a branch instruction.
 

Assembly language instructions for control of execution

Unconditional jump

A jump instruction puts the address of a label into the PC. Execution continues from that point. jar also saves the old PC value as a "return address" in register $ra ($31). This is used for procedure call, see chapter 8.
 

Conditional branch

These instructions branch, that is, change the PC to the label, when a condition is true. The condition is always a comparison of 2 registers, or a register and a constant. Normally, they are compared as signed numbers. Where it matters, you get an unsigned compare by ending the operation code with a u.
 

Instruction	Branch to label if		Unsigned
beq Rsrc1,Src2,label	Rsrc1 = Src2
bne Rsrc1,Src2,label	Rsrc1 <> Src2
blt Rsrc1,Src2,label	Rsrc1 < Src2		bltu
bgt Rsrc1,Src2,label	Rsrc1 > Src2		bgtu
ble Rsrc1,Src2,label	Rsrc1 <= Src2		bleu
bge Rsrc1,Src2,label	Rsrc1 >= Src2		bgeu

 

Comparison with zero is useful, and can be done simply by using $0 as Src2 (remember, it always holds the value 0). For your convenience, you can write comparison with zero by putting a z at the end of the operation code. Thus these two instructions are the same:

               blt  $t0, $0, cold
               bltz $t0, cold

(You can't use both u and z. There would be no point.)

These are all the instructions you need to write very complicated programs. In fact, you can write programs that are too complicated with them, so complicated that you have to explain the flow with so many arrows that your paper looks like a bunch of spaghetti. You must avoid "spaghetti programs" and use the well-known, disciplined constructs you have learned in your other programming classes.
 

IF constructs: choosing alternatives

In an IF statement, you "branch around" a section of code. In an IF - THEN - ELSE construct, one of two alternatives is executed. Here are some pseudo code examples, with assembly language translations. (Assume that swim and cycle are labels of .asciiz strings containing the phrases.)

IF num < 0 THEN
  num := - num
ENDIF
{absolute value}
                                IF temperature >= 25 THEN
                                    activity := "go swimming"
                                ELSE
                                   activity := "ride bicycle"
                               ENDIF
                               print (activity)
    lw   $t0, num
    bgez $t0, endif0
  # must be ltz------
     sub  $t0,$0,$t0   # 0-num
     sw   $t0, num
endif0:
  #  num is now guaranteed non-negative

                                lw  $t0, temperature
                                blt $t0, 25, else25
                                la  $a0, swim
                                j   endif25
                            else25:
                                la  $a0, cycle
                            endif25:
                                li  $v0, 4   # print string call code
                                syscall
 

Note that the assembly "branch around" is the opposite of the high-level condition. Also note the jump instruction needed before ELSE.
 

Loops: repetition

If a jump (or branch) reloads the PC with a lower address, that instruction will be reached again, and again... A loop results, as the same block of instructions is repeated. One must be careful to avoid an infinite loop by providing a branch out of the repetitive region that will eventually be taken. Two well-known and well-behaved constructs are WHILE and FOR. FOR is actually a special case of WHILE that uses a counter. Both are pre-test loops, the test (branch
instruction) comes at the beginning of the loop body, and there is a jump instruction at the end.

{sum non-negative numbers}
sum := 0
num := 0
WHILE num >= 0 DO
    sum := sum + num
    read (num)
ENDWHILE
                                   {write 10 lines}
                                   FOR countdown := 10 downto 1 DO
                                      print ("Hello again...")
                                   ENDFOR
#   add    $t0, $0, $0 really:
move   $t0, $0   #sum=0
move   $v0, $0   #num=0
while5:
      bltz   $v0, endwhile5
      add  $t0, $v0
                    #$v0 switches role here
      li   $v0, 5   #read int call
      syscall
      j  while5
endwhile5:

                                  # set up print arguments before loop
                                  la  $a0, hello_again
                                  li  $v0, 4    #print string call

                                  li  $t0, 10   # countdown
                                  for10:
                                       beqz  $t0, endfor10
                                       syscall   #print another line
                                       sub $t0, 1    #decr. countdown
                                       j  for10
                                  endfor10:

A REPEAT loop is a post-test loop. It may be used in special situations when it is known that the loop body should be executed at least once.

    Embarrasing historical note: The first version of FORTRAN implmented FOR loops as post-test loops. As a result, they always executed once even if it made no sense. It took 20 years to correct the situation.
 
 
 

Instruction formats and addressing modes

We now know enough instructions to write reasonable programs. It is time to look at various ways to refer to data, and at how machine instructions are encoded. This will give us insights into what hardware designers have to do, and explain why they have chosen to omit certain reasonable (from the programmers point of view) instructions from the instruction set. We have already seen some of these conversions. First, lets look at MIPS instruction formats.
 

    Instruction formats

•         register
•         immediate
•         jump

    Addressing modes

•         immediate - value built in to the instruction
•         register - register used for data

    Memory refrencing - used with load and store instructions

•         label     - fixed address built in to the instruction
•         indirect - register contains the address
•             Base addressing - field of a record
•             Indexed addressing - element of an array

Instruction formats

To keep the MIPS processor simple and fast, all instructions fit in 32-bit words, and there are just 3 different instruction layouts. Decoding of instructions starts with the leftmost 6 bits, the operation code. This determines how the rest of the bits will be handled. The formats are:
 

Register

For operations using only registers as operands, the operation code is 000000
 

6 bits	5 bits	5 bits	5 bits	5 bits	6 bits
000000	source reg	target reg	Destination	shift amt	function
000000	01010	00111	00101	00000	100010

The last line of the table gives as an example a subtract instruction, sub $5, $10, $7
 

•     3 five-bit fields identify the 3 registers used for the operation. Note the order is different from Assembly language, the 2 sources come first, then the     destination. The "target" is usually the second source, but in some instructions it is the destination or has an alternate meaning.
•     Shift amount is used in the shift instructions.
•    Function determines just what is done with the registers, usually it is an arithmetic or logical (boolean) instruction

This diagram shows how data flows from registers to the ALU (Arithmetic Logic Unit) and the result is stored back into the destination register, for the instruction

Immediate

Some instructions include a constant value. This constant is included right in the instruction, so it is called an immediate value. In 32 bits, there is room for a 16 bit immediate, 6 bits of op. code, and 2 register numbers (5 bits each). A good example is add immediate (addi), which adds source register + immediate and stores in target register. Since the immediate value is shorter than the register, it is "sign-extended" to form a 32-bit signed number. Thus addi $t1,$t2,0xfffe (shown in table) actually adds 0xfffffffe, which is -2.
 

This layout is also used for load, store, and branch instructions. (see diagram for store)
 

•     In load and store, the immediate value is added to the source register to form the memory address of the data.
•     In branch, the immediate value is an offset (in words) from the present PC value.

Jump

The jump instructions (j & jal) use all 26 bits following the op code for the address to jump to. Since all instructions are word aligned, the last 2 bits of the
address are always 0, so they are left out of the instruction. Upon execution, the 26 bit jump target is shifted left 2 bits, and stored in the PC, this causes the jump
to take effect.

    Effectively this is a 28-bit address, so jumps can "only" target the first 256 Mbytes of memory. This could be a problem for the operating system of a machine with more that this amount of memory. Such a machine would  probably be manipulating massive amounts of data, and so could reserve the "low" memory for programs. Alternatively, compilers could be directed to use jump-register instructions or branch-always instructions instead of jumps.

Addressing modes

There are a number of ways to refer to data, either as source operands, or destination locations for storage. This section starts with these different methods from the programmers point of view, and discusses how these are encoded in the MIPS instruction formats.
 

Immediate

Source operands can be constants. A constant value is usually encoded directly in the machine language instruction, so that it si available immediately after the instruction is decoded, without fetching it from memory. Understandably, this does not provide any location for storing data.

MIPS instructions encode immediate constants in the lower 16 bits of the immediate instruction layout. For constants larger than 16 bits, the assembler generates 2 machine instructions, the upper half of the constant is loaded into the $at register with the "load upper immediate" instruction.

Examples of instructions with immediate data:

     addi $t0,t1,65
    sub  $t0,7                 #assembled as:
 

    addi $t0, $t0, -7
    li   $t3, 0x12345678      #assembled as
 

    lui  $at, 0x1234
    ori  $t3, $at, 0x5678     #puts it all together
    bgez $t5, 16              #skip 4 instructions ahead if $t5
                              #is non-negative   (4 is encoded in
                              #immediate field)

The last example is also referred to as PC-relative addressing, because the immediate value is (shifted left 2 bits and) added to the PC when the branch is taken. The constant is often referred to as an offset or displacement. It is a signed number, so the new PC value can be before (a loop) or after the current instruction.

This mode is very useful because the operating system can move the program to another part of memory without affecting branch instructions.

Most processors use PC-relative addressing for branch instructions. The number of bits used for the displacement limits the distance to the branch target. In older designs, such as the 6502 and 80x86, 8 bits are used, limiting the displacement to + or - 128 bytes before or after. This usually caused students some distress.
With MIPS, the limit is 128Kbytes. Since branch instructions are usually used within procedures, this is unlikely to cause you any problems!
 

Register addressing

Registers may be used as sources and destinations of data. Access to registers is extremely fast, much faster than fetching data from memory. All the instructions listed above reference 1 or 2 registers as well as the immediate constant. In addition, many instructions reference registers exclusively. Most processors require at least one operand of arithmetic instructions to be in a register. Instructions with all operands in registers (or immediate) are the fastest to execute.

MIPS provides 32 registers, and encourages you to load your data into them and work with it there, resulting in very fast execution. Since it takes only 5 bits to specify a register, as opposed to 32 bits for a memory location, the register instruction layout can easily accomodate 3 register designations.

Examples of register instructions:

    addu $t3, $t1, $t2       # add (unsigned) $t3 := $t1 + $t2
    sub  $t0, $t3            # subtract (signed) $t0 := $t0 - $t3
 

Memory addressing

With 32 bit addresses, a computer can access as much memory as you can afford to buy. Well, up to 4 Gigabytes. You can store lots of data there, and transfer it to and from the processor as needed. In return for large amounts of storage, access is slower. Typically an instruction will allow access to at most one memory address. MIPS, in common with other RISC processors and most supercomputers, restricts this to load and store instructions. There are several ways we could
specify the address:

label - fixed address built in to the instruction

Also called direct addressing, the known address can be built into the instruction as a constant. Programers usually specify this address using a variable name or label in the data segment, the compiler or assembler assigns it a numeric value. Since it is a 32-bit value, a MIPS assembler will break it into two 16-bit immediate quantities, and assemble 2 machine instructions to do the job. Examples:

    lw  $t0, MyNumber       #load the word into $t0
    sb  $t9, firstInitial   #store rightmost 8 bits of $t9 in data segment

indirect - register contains the address

Besides holding data, a register can be used as a pointer, holding an address that points to the data. The data is transferred by putting the register;s contents on the address bus, the data is transferred on the data bus. This is called indirect addressing because the register itself is not the target, rather it points to the target in memory indirectly. A common use of this is to step through a string one character at a time. One first loads a register with the address of the string, and then
uses it to access the characters in succession, incrementing the register each time. For example, suppose we have the string

    catStr:  .asciiz   "cat"

The address can be loaded into a register with the load-address instruction (in machine language it is just like load immediate, except the constant is the address rather than data), and then refer to the characters indirectly

    la  $t0, catStr
    lb  $t1, ($t0)        # 'c' is now in $t1
    addi      $t0, 1      # point to next character
    lb  $t2, ($t0)        # 'a' is now in $t2
 

Base addressing

A variation of indirect addressing is useful for referring to fields of a record or struct. Suppose we store telephone numbers in a record of 4 short integers (16-bit halfwords), holding area code, prefix, 4-digit number, and extension. Then the extension number starts 6 bytes from the beginning of the record. We can get it by adding the offset 6 to a register pointing to the record:

    la    $t0, MyPhone     # $t0 points to a telephone record
    lh    $t1, 6($t0)      # $t1 loaded with the extension # in that record
 

Indexed addressing

Suppose we want to index an array. We know the address of the (start of) the array, and want a register to index it. Now the address is fixed, and the register will hold a variable offset. The following code will copy 10 bytes (the assumed length of both strings, including final 0) from str1 to str2, using $t0 going from 9 downto 0

      li   $t0,9           # t0 indexes arrays
copyloop:
      lb   $t1, str1($t0)  # t1 used to transfer character
      sb   $t1, str2($t0)  #    to str2
      sub  $t0, 1          # decrement array index
      bgez $t0, copyloop   # repeat until t0 < 0

Note that if we were moving words, we would need to decrement the index by 4 instead of 1.

To implement this in MIPS, the assembler needs to produce 3 machine instructions for each indexed instruction, beacuse the 32-bit constant address must be split into 2 16 bit immediate values.
 

The bottom line - MIPS memory addressing

MIPS, in keeping with the RISC philosophy, actually has only one memory addressing mode at the machine level, it corresponds to base addressing. Indirect addressing is simply a special case with offset = 0. Direct and indexed addressing both involve fixed 32-bit addresses, the assembler calculates these numerical addresses and splits them into 16-bit sections. The high order part goes it $at using the lui instruction, the low order part ends up in the immediate field of the
machine load or store instruction. The sb instruction above assembled as follows, str2's address was 0x1001000c (0x1001 = 4097)

0x3c011001  lui $1, 4097 [str2]             ; 7: sb   $t1, str2($t0)
0x00280821  addu $1, $1, $8
0xa029000c  sb $9, 12($1) [str2]

You can figure out how this has the same effect as if we had been able to code directly

            sb $t1, 0x1001000c($t0)

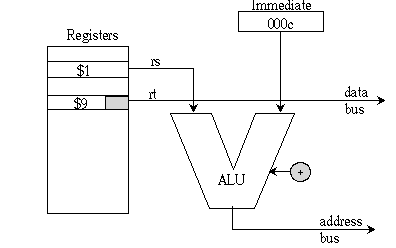
Meanwhile, here is the layout of the actual sb $9, 12($1) base addresssed instruction, and a diagram explaining how the immediate 12 is added to $t0, the sum placed on the address bus, and $t1 (a character) on the data bus.
 

MIPS function call and return

When we call a function (procedure, subroutine), we normally want to come back to the place we left, the following instruction. To do so, we need a means of remembering our place, so the function can return to it. Some convention needs to be agreed upon as to where to store a return address. Some conventions that are in use are:
 

•     The upper left-hand corner of the envelope, for a letter sent by Canada Post,
•     The word preceeding the jump target, in a computer program
•     the top of a stack data structure, which has the LIFO (last in first out) property
•     A designated register.

MIPS uses register 31 as the return address register

We have actually seen the jump instructions involved in function call and return, they are:
 

•     jal - jump and link. It has the same format as jump. In addition to jumping, it stores the return address, that is the address of the following instruction, in register 31, named $ra, the return address register.
•     jr - jump register. Instead of a fixed target address, given as a label, this instruction jumps to the location contained in a register. jr $ra in particular  jumps back to the location last saved in the return address register.

As an example, we could have a simple function to print an integer, that takes care of the detail of remembering the system call number, and another to print an end-of-line character:

    print_int:              endline:
           li  $v0, 1               la  $a0, endl  #define in .data as "\n"
           syscall                  li  $v0, 4
           jr  $ra                  syscall
                                    jr  $ra

    These can then be called to output some numbers

        li  $a0, 42        # writeln (42)
        jal print_int
        jal endline
        li  $a0, 1999      # writeln (1999)
        jal print_int
        jal endline

This suffices for a main program calling functions sequentially. However, it does not allow for a function to call another function, so later on we will see how to save return addresses systematically, using a stack.

EXAMPLE CODE:
    SUMS.ASMSUMSHEX.ASM
 

Bit Fiddling operations

•     Shifting (and rotating)
•     Logical (Boolean) operations

So far we have been manipulating numbers, in sizes of either bytes or words. In this section, we will look at the operations that are usually provided for working with individual bits. There are several reasons for doing this. One can compress data, using only as many bits as necessary, so several fields can share the same word. We have seen that instruction layouts divide a word up like this. An assembler must put the elements of an instruction together, for example, lining up the
5-bit fields for registers and combining them.

Multiplying and dividing by powers of 2 is also easily done simply by shifting bits. Adding a zero on the right of a binary number multiplies it by two, just as adding a zero on the right of a decimal number multiplies it by 10. A shift left instruction is handier, and often faster, than setting up a divide operation. Let's look at the bit-fiddling operations, and how they are implemented in MIPS instructions.
 

Shifting operations

By shifting we mean moving all the bits in a word either right or left. Think of them as books filling a shelf. If we push them all over, some books will fall off the end, and be lost. There will be space available on the other end. Since a word is always 32 bits, we need to put something in that space. In a logical shift, the empty positions are filled with 0's. If you shift a word 32 or more bits, it will contain all 0's. In a rotate operation, the bits falling out one end are replaced at the other end. (Think of picking up each book as it falls off the shelf, and replacing it at the other end.) As a result, no bits are lost, and rotating a word by 32 bit positions restores its original value.

All processors, so far as I know, have shifting hardware, and instructions, capable of shifting at least 1 bit left or right. There doesn't appear to be any reason to shift a 32 bit word by more that 31 bits, any more than one would need to set an ordinary clock 50 hours ahead. You could just set it 2 hours ahead.

Here are some examples of shift and rotate operations, each starting from the same bit pattern. I hilighted 3 bits, so you can see their new locations. The new filler 0000's are in italics

Before:             11011011011011011011011011111111

Shift right 6      00000011011011011011011011011011

Shift left  5       01101101101101101101111111100000

Rotate left 4       10110110110110110110111111111101 <-- leftmost 4 came here

So, it is possible to get any bit into any position, bringing other bits along the same distance, and either losing bits of the end, or replacing them at the other end.
 

Arithmetic shifts (signed numbers)

Adding a zero on the right of a binary number multiplies it by two, as I mentioned. By shifting a number 1 bit left, each bit has twice the place value it had before, and we bring in a 0 to hold the units place. Multiplication by any power of 2 is possible in this way. For instance, to multiply by 16, shift left 4 bits. Example, 7 * 16

    7 * 16  =  111 * 10000  =  1110000  = 0x70  =  112

Conversely, shifting right divides. Any remainder is thrown away with the discarded bits. 127 / 8, shifting right 3 bits:

    01111111  --->  00001111   =  15

There are some special considerations for arithmetic shifts.
 

•     Shift right arithmetic: For a negative number, shifting 0 bits in from the left will change the sign bit to positive, this is clearly wrong. The solution is to "sign  extend" the number, by filling in with the sign bit, either 0 or 1 as the case may be.
•     Shift left arithmetic: If any significant bits are shifted out, the answer will be wrong, and we would like to know about it. If the number is positive, we don't want to lose a 1 bit, or have a 1 bit end up in the sign bit, making the result negative. We would like to know if either of these overflow conditions occurred. The actual shift is identical to shift left logical. Some processors set a "flag" to indicate overflow. Programmers typically ignore such flags. MIPS simply does not have a special shift left arithmetic instruction

-38  =  11111111111111111111111111011010,  divide by 4, shift right aritnmetic 2

gives   11111111111111111111111111110110,  which is -10

Now, you may not quite agree with that answer. It makes mathematicians happy, because it agrees with the remainder of +2, that is, -10*4 +2 = -38. The answer has been truncated in the negative direction. Computer scientists are divided, and in fact some hardware gives this result for division, and some gives -9. In fact the MIPS architecture does not specificy how negative integers should be divided. As for the SPIM simulator, it simply uses the divide instruction of the "host"
processor, so results of divide instructions can vary! Not so when you divide by shifting, you will always get the "mathmatical" result we have just seen.
 

MIPS shift instructions

The format of these instructions is: op code, Destination register, source register, shift amount. The shift amout is usually a constant, 1-31 bits make sense. It may also be contained in a register (variable shift). Examples, source is $t0:

        sll  $t4, $t0, 5     #shift left logical 5 bits (multiply by 32)
        sra  $t5, $t0, 2     #shift right arithmetic 2 bits (divide by 4),
                             #sign extended
        srl  $v0, $t0, 1     #shift right logical 1 bit. Sign bit is now 0
        srlv $v0, $t0, $t1   #shift right logical, $t1 says how many bits
 
 

Logical operations - Boolean Algebra

Today's digital computers are composed entirely of logical circuits, called gates. These gates use 1 or more transistors to implement the logical operatios AND, OR, and NOT. A variation on (inclusive) OR is eXclusive-OR, usually written XOR. These are also called boolean operations, after George Boole, originator of "The Algebra of Truth."

Boolean algebra deals with two values, FALSE and TRUE. Since boolean values can be encoded in 1 bit, we can do so, and by convention 0 represents FALSE and 1 represents TRUE. The operations can be defined by enumerating all the possible values of operands and results in a "Truth table"

NOT simply reverses the value. NOT 0 = 1, and NOT 1 = 0

Some laws of boolean algebra, these identities can be verified using truth tables: (In these laws, + means OR, a bar over something means NOT, while AND is shown like multiplication in algebra, by writing two terms together.)

     A 1 = A         A + 0  =  A                   identity
     A 0 = 0         A + 1  =  1                   null
     A A = A         A + A  =  A                   idempotent
     A(A + B) = A    A + AB =  A                   absorption
       _                         _
     A A  = 0                A + A  =  1           inverse
     AB  =  BA               A + B = B + A         commutative
     (AB)C = A(BC)           (A+B)+C = A+(B+C)     associative

     A(B + C) = AB + AC      A + BC = (A + B)(A + C)    distributive
     ____   _   _             _______   _  _
     (AB) = A + B             (A + B) = A  B       de Morgan

NOT (A AND B) = (NOT A) OR (NOT B)    1st deMorgan in Pascal notation
           _         _
A XOR B = (A B) + (A B)               XOR Defined in terms of other operations

The deMorgan laws are of particular importance to programmers, they show an important relationship between AND, OR and NOT. When NOT is distributed over an expression, AND exchanges with OR. This is worth considering when constructing WHILE loops. Here is the proof of one by truth table:

Compilers will store boolean values in a byte or word holding either a 0 or 1, this wastes some space. An array of boolean may be packed 32 values to a word, and shift instructions used to extract specific values. Usually any non-zero value will evaluate to TRUE because beqz, bnez instructions will be used.

The important point about logical instructions in assembly language is that they operate on all corresponding bits of the operands in parallel. There are no carries or other interaction between different bit positions.

MIPS logical instructions are all the 3 operand format, just like add and sub. Like them, the second source can be a constant. (Well, of course not only has destination and source registers. It is actually implemented by nor (not or) that follows the usual pattern.)
 

Masking

A common use of logical operations is isolating, or "masking" parts of words. Just like a mask covers your face and lets your eyes show through, a bit mask lets some bits show through, and hides others. Think of one operand as the "data" and the other as the "mask". This is a consequence of the identity and null laws above. For the different operations:
 

•     AND - for every 1 in the mask, the data bit shows. For every 0 in the mask, the result is 0, the data bit is hidden.
•     OR   - for every 0 in the mask, the data bit shows. For every 1 in the mask, the result is 1, hiding the data bit.
•     XOR - for every 0 in the mask, the data bit is unchanged. For every 1 in the mask, the data bit is reversed. If you XOR twice, the original value is     restored. This property is often used in graphic programming to show moving objects. If something is put into an image with XOR, another XOR will remove it. If you see something that changes colours to contrast with whatever background there is, XOR operations are being used.

Example: Find the Source Register in an instruction

0x214afff3 addi $10, $10, -13

Instruction in binary:  00100001010010101111111111110011
Mask:                   00000011111000000000000000000000
Result of AND:          00000001010000000000000000000000
Shift right 21 bits     00000000000000000000000000001010

And we have the source register number, suitable for printing with syscall service 1.
 

Example: Changing case of letters

In order to make case-insensitive comparisons, both items being compared need to be in the same case. Only the letters should be converted, of course. By looking at the ASCII code chart, we see the only difference between the upper case and lower case letters is bit 5. To make a letter:

    lower case, force this bit to be 1, by ORing with  00100000 = 0x20
    upper case, force this bit to be 0, by ANDing with 11011111 = 0xDF
    the opposite case, change this bit, by XORing with 00100000 = 0x20
 

Example: Binary digit to ASCII character

Suppose we believe that register $t0 contains a binary number that can be represented by a single digit, 0..9. (This would be true for the remainder of division by 10.) From the ASCII table, we see that the numeric characters '0' .. '9' are the hex values 0x30 .. 0x39. All we have to do is OR the register with 0x30, and we have the required character, suitable for storing in a string.

                or  $t0, 0x30      #binary number to ASCII character
 

Example: Binary 4 bits to ASCII character for Hexadecimal - '0' .. '9' 'A' .. 'F'

If we want to represent 4 bits as a hex digit in a string, this isn't quite good enough, because the ASCII code 'A" doesnt follow immediately after '9', instead, there is a gap of 7 other characters. The solution is to test and add 7 if necessary. It is also a good idea to make sure only the lowest 4 bits are non-zero. In this coding example, we show what happens to the value 13, in binary 1101, in $t0:

     and   $t0, 0x000f      #00001101  only allow lowest 4 bits non-zero
     or    $t0, 0x30        #00111101
     ble   $t0,'9', numeric #00000111   to be added, since > '9'
        add  $t0, 7         #01000100   ASCII 'D'
numeric:
 
 
 

Example: Convert word to Hex string, 8 digits

This example uses the single digit conversion code above, and fills a string of 8 characters with the correct hex digits. To do this we need to shift the word being converted 4 bits right each time, apply the "binary to hex" conversion, and store the resulting character in the string right to left.

# function to convert word value to a hex string. Returns pointer to the string
#    arguments:
#        input:  a0, word to be converted
#        output: v0, pointer to the string
#    registers used:
#        t2 - working copy of word
#        t1 - point to string characters, right to left
#        t0 - single 4-bit value, converting to character, as above

word2hex:
    la     $v0, str8            #string workspace defined in data segment
    add    $t1, $v0, 8          #point to last character position + 1
    move   $t2, $a0             #copy input, will be shifting $t2
hexloop:
      sub    $t1, 1             #point 1 character left
      and    $t0, $t2, 0x000f   #only allow lowest 4 bits non-zero, converting in $t0
      srl    $t2,$t2, 4         #shift copy of word so next 4 bits are on right
      or    $t0, 0x30           #make it numeric ASCII character, but ...
      ble    $t0,'9', numeric   #IF > '9',
        add  $t0, 7             #must add 7 to get 'A' .. 'F'
numeric:
      sb     $t0, ($t1)         #store hex character in string
      bne    $t1,$v0, hexloop   #UNTIL all 8 characters stored
    jr     $ra                  #RETURN from function call, $v0 points to string

A fully running version using this code is hex1.asm
 

--------------

Function calls, and the stack

• case study: URL encoding function, which in turn calls
• bin2hex - convert 4 bits to a "hexadecimal" character (0-9, A-F)
• AlphaNumeric - boolean valued function to tell if a character is in fact a letter or number.
• conventions for register usage
• the Stack
• Putting it all together

Case Study: URL encoding

Anyway, this is complex enough that it will pay to structure the problem of producing a URL-encoded string by calling some sub-functions. The ones that come to mind are:

• bin2hex - convert 4 bits to a "hexadecimal" character (0-9, A-F)
• AlphaNumeric - boolean valued function to tell if a character is in fact a letter or number.

URLencode (plain, encoded)
FOR each character ch in plain, store in encoded,
   CASE ch OF
      space:        '+'
      AlphaNumeric: ch
      (other):      '%'
                    bin2hex (left nibble of ch)
                    bin2hex (right nibble of ch)
END FOR

To start with, let's get the little functions on the table. Here is

bin2hex

# char bin2hex (binary) converts 4 bits (least significant) of input to an
#                       ASCII character giving the hex value. '0'-'9' or 'A'-'F'
# registers:
#       $a0, input argument, unchanged
#       $v0, char value returned
#       no other registers used

bin2hex:
        andi    $v0, $a0, 0x0f  # mask off 4 lower bits
        ori     $v0, $v0, 0x30  # make it ASCII digit
        ble     $v0, '9', numeric       #if hex value A..F, then
          add   $v0, 7                  # add 7, since there are 7 characters
numeric:                        # between '9' and 'A'
        jr      $ra             # RETURN

---

AlphaNumeric

This could be done "on the fly" by careful arrangement of 6 branch instructions. There is a more reliable way, now that we know about the logical instructions. It involves a new bunch of instructions, the "set" instructions, which are similar to "branch" in that they compare two operands, but instead of branching, they store the boolean result in the desination register. We then use boolean instructions with these values. Here is how the code starts, ch in $a0:

        sge     $t5,$a0,'A'
        sle     $t6,$a0,'Z'
        and     $t7,$t5,$t6     #(ch >= 'A' and ch <= 'Z')

#############################################################
# boolean function AlphaNumeric (ch)
#       $a0: argument ch, unchanged
#       $v0: boolean value output, TRUE (1) if ch is letter or number
#       Uses registers t5, t6, t7, t8
#############################################################
AlphaNumeric:
        sgt     $t5,$a0,0x40    #ch > 'A'-1
        slt     $t6,$a0,'Z'+1   #ch < 'Z'+1
        and     $t7,$t5,$t6     #(ch >= 'A' and ch <= 'Z')
        sgt     $t5,$a0,0x60    # ch < 'a'-1
        slt     $t6,$a0,'z'+1
        and     $t8,$t5,$t6     #(ch >= 'a' and ch <= 'z')
        or      $t8, $t8,$t7    # $t8 = big or small letter
        sgt     $t5,$a0,0x2f    #  ch > '0'-1
        slt     $t6,$a0,'9'+1
        and     $t7,$t5,$t6     #(ch >= '0' and ch <= '9')
        or      $v0, $t8,$t7    # $v0 = AlphaNumeric truth value returned
        jr      $ra

Conventions for register usage

• $a0, $a1... to hold function arguments (input values, pointers)
• $v0 [,$v1] for value(s) returned by a function
• $t0 - $t9, the temporary registers, may be freely used by a function. Your values may be trashed.
• $s0 - $s7, the saved registers, will not be altered by a function you call, your values are safe. (Providing the author of the function respects the convention!)

Therefore, we only need to save $ra (we want to return to our caller, obviously!) and $a0 (to be nice to our caller, who may expect the pointer to the plain string to still be there.) Now, lets consider where we can store these things:

1. We could declare variables in the data segment for each register to be saved by each function. This gets messy. And it doesnt work if a function calls itself.

The Stack

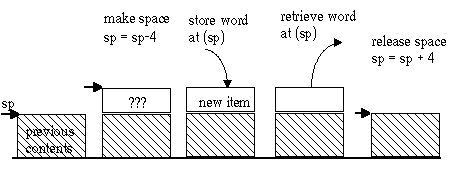
By custom, computer stacks grow "downward" from higher to lower memory addresses. The stack pointer always points to the top word on the stack. The permitted stack operations are:

• push: To place a new item on the stack, the stack pointer is first decremented, and then the item is stored at the new location pointed to.
• pop: To remove an item from the stack, the value pointed to by the stack pointer is copied (usually into a register), and then the stack pointer is incremented, exactly reversing the push operation.

This figure shows the operations on a stack. In any 32-bit machine, a 32 bit word is always pushed or popped, so the sp is always kept a multiple of 4.

CISC processors typically have instructions that implicitly manipulate the stack pointer, usually named SP. They are PUSH, POP, CALL and RET. The last two store and retrieve return addresses directly to and from the stack.

In MIPS, the stack pointer is $29, named $sp. It is only made special by the fact that the operating system sets up the stack for you, with $sp pointing to the initial top of stack. To push, the sequence is

sub   $sp, 4      #PUSH on the stack
sw    $ra, ($sp)  #our return address

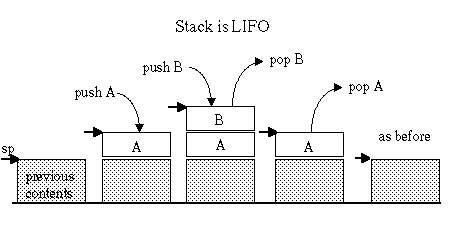
lw    $ra, ($sp)  #POP our return address from the stack
add   $sp, 4      #top of stack back as it was before the PUSH

URLencode:
# function URLencode (plain, encoded, maxlength)
########  entry code: save registers
        sub     $sp, 4          # PUSH return address
        sw      $ra, ($sp)
        sub     $sp, 4          # PUSH  a0
        sw      $a0, ($sp)      #   (be nice, restore caller's register)
########################

############ exit code: restore registers, POP in reverse order to PUSH
endURL:
        lw      $a0, ($sp)      # POP start of string addr
        add     $sp, 4
        lw      $ra,($sp)       # POP return address
        add     $sp, 4
        jr      $ra             ##### return, using newly restored $ra

Putting it all together

The whole thing, including a main program to test it out, has a few extra refinements, added after the basic algorithm was implemented. A third argument, $a2, specifies the maximum space available for the output string. This is good safe programming practice, as otherwise other variables could be overwritten, with usually bad results. At the beginning of each successive loop iteration, we make sure there is space for 4 characters, %hh, and a null byte.

Recursion

It is defined recursively as:

0! = 1
n! = n * (n-1)!   for n > 0

Implementation

• The return address must be saved on the stack
• Space for local variables must be allocated on the stack, either directly, or indirectly, by using the s-registers, and saving their contents before use. (Fixed locations in the data segment cannot be used)
• And remember to test for the base case.

Historical note:

Factorial function

int factorial (int n){
    if (n < 2) return 1;
    return (n * factorial (n-1));  /* n! = n * (n-1)! */
}

factorial:
    bgtz  $a0, doit
        li   $v0, 1      # base case, 0! = 1
        jr   $ra
doit:
    sub  $sp,8           # stack frame 
    sw   $s0,($sp)       # will use for argument n   
    sw   $ra,4($sp)      #  return address

    move $s0, $a0        #  save argument
    sub  $a0, 1          #  n-1
    jal  factorial       #  v0 = (n-1)!
    mul  $v0,$s0,$v0     #     n*(n-1)!

    lw   $s0,($sp)       # restore registers from stack
    lw   $ra,4($sp) 
    add  $sp,8
    jr   $ra

Excescise: Modify this code so that $a0 is restored, by pushing and popping it. You shouldn't have to use $s0 or any more stack space than at present, but be careful where your pushes and pops go.

The towers of Hanoi

1. Move only one ring at a time
2. A ring may never sit on top of a smaller ring

MoveStack(pegs: soruce, destination, spare; integer numberrings)
    MoveStack (source, spare, destination, numberrings -1)  #get all but bottom ring out of the way
    MoveRing  (source, destination)                         #move the bottom one
    MoveStack (spare, destination, source)                  # and pile the rest on top

• hanoi.a, by John Waldron, in the textbook. Uses $s registers saved on the stack. Elegant printout.

Quicksort

Partition:

• All elements < pivot
• All elements > pivot

Then just Quicksort each of these smaller arrays

Finally, stick the smaller arrays and pivot together. Hoare defined Partition (for arrays) so that this is automatic.(No, I am not going to code it in assembly language in this millenium.)

------

Floating point operations (3.14159)

Very big and very small numbers can be expressed more conveniently in "scientific" notation, using some significant digits multiplied by a power of 10, for instance

       1.2×108     0.123456×10-27     -30.09×1030

The important points to remember are:

• Floating point represention of 3.0 will be a quite different bit pattern from the integer 3
• "Real" numbers can only be represented to a certain precision, approximately 6 decimal digits for 32 bit "single precision." Operatiions cannot be counted upon to give totally precise results. Even so simple a number as 0.1 cannot be represented exactly! (Just as 1/3 cannot be represented exactly in base 10.)
• A limit is imposed on the size of the exponent

MIPS floating point operations

As advancing technology allows more circuit elements on a chip, the "copressor" functions are coming to be incorporated in the main processor chip. Earlier and less expensive personal computers often lacked a floating point processor, this lack was made up by software implementing the floating point operations, at a much slower speed. For those familiar with the Intel processor family, the 80386 and its coprocessor, the 80387, were combined into the 80486 chip.

• single, using a single 32-bit word, and
• double - 64 bits.

Doubles can be used to particular advantage in intermediate calculations, in order to minimize accumulation of error, particularly the possible loss of accuracy when subtracting nearly-equal numbers. Operations with doubles are denoted with the suffix .d in the op code, I will not discuss them further here.

Input and output:

• Service 2, print_float, prints the single precision value in $f12
• Service 6, read_float, allows user input of a real number, which is returned in $f0

Load and store

l.s    FRdest, address       # Fregister := memory
s.s    FRsrc,  address       # (left to right) memory := Fregister

l.s    $f2, pi               # load constant from memory
li     $v0, 6                # read diameter
syscall                      #  ... into $f0

mul.s  $f12, $f0,$f2         #(see below) circumf := diameter * pi
s.s    $f12, ($t0)           # store in an array location

li     $v0, 2                # print diameter
syscall

--------------

pi:   .float  3.14159             # assemble a single float in data segment

Floating point arithmetic operations

The 4 branches of arithmetic: ambition, distraction, uglification, and derision. - Lewis Caroll

add.s   FRdest, FRsrc1, FRsrc2
sub.s   FRdest, FRsrc1, FRsrc2
mul.s   FRdest, FRsrc1, FRsrc2
div.s   FRdest, FRsrc1, FRsrc2

In addition, these 2-operand operations are available:

abs.s   FRdest, FRsrc       #absolute value
neg.s   FRdest, FRsrc       #negate (change sign)
mov.s   FRdest, FRsrc       #move, note the lack of 'e'

Conversion: Integer <---> Floating

Type conversions are the responsibility of the Floating point coprocessor, and are done with data in the F-registers.The instructions are of the form

cvt.s.w   FRdest, FRsource

Converting integer to floating transforms the bit pattern used, but preserves the numeric value of small integers (up to about 6 digits). Converting from floating to integer, on the other hand, causes any fractional part to be lost (truncated), and if the floating number has a very large magnitude, perhaps its value cannot be stored as an integer.

In this example, we convert pi = 3.14159 to an integer, with the value 3:

l.s      $f0, pi
cvt.w.s  $f1,$f0   #now $f1 = 3 (integer) and cannot be used by the coprocessor

Moves to and from the coprocessor

The instructions for moving data between general registers and coprocessor registers are:

• mtc1   Rsrc, CPdest    #note, left to right!  move to coprocessor one
• mfc1   Rdest, CPsrc    # move from coprocessor one

Example: continuing from above, to calculate the radius of the circle (diameter/2), from the diameter in $f0:

li   $t1,2      #integer 2
mtc1 $t1,$f1    #integer 2 arrives in coprocessor
cvt.s.w  $f3,$f1  #single 2.0 in $f3
div.s    $f3,$f0,$f3  # radius in $f3

Compare (and branch) with floating numbers

The compare instructions have the form   c.condition.s  FR, FR   with 3 of the expected 6 conditions implemented. Instead of .s you may also use .d   The 3 forms are:

c.eq.s
c.le.s
c.lt.s

Example:

# IF x > y THEN k = 1 ELSE k = 2    x in $f1, y in $f2
     c.lt.s  $f2, $f1         # y < x  is same as  x > y
     bc1f  else
           li  $t0,1          #THEN k = 1  (in $t0)
           b   endif
else:
           li  $t0,2          #ELSE k = 2
endif:

A final word of caution about equality

(x == 1.0) is more safely written as abs(x-1.0) < 0.000001
 
 

Other processor architectures and assembly languages

You will observe that in all instruction sets, there are groups of instructions for: Moving data, arithmetic, jump, compare, branch, logical, and shift. There also may be operations affecting the stack, and for input/output.

A) Processor size, the external view

• The size of the Data Bus determines how many bits may be transferred at one time. Common sizes are 8, 16, and 32 bits.
• The size of the Address Bus determines how many memory locations may be accessed. If there are n bits (wires) in the Address bus, there must be 2ⁿ possible addresses. This is referred to as the Address Space. While not necessarily true, all the processors listed below can access single bytes of memory, so the address space is in terms of bytes.

B) The internal view: Registers and instruction sets.

All processors have a program counter, usually named PC. It needs to have the same effective size as the Address Bus. Then they have some "general purpose" registers that can hold addresses and data. In addition, the intel 80x86 series (including the Pentium) have 4 or 6 "Segment" registers, which are used to extend the address space.

6502

• A, the accumulator, used by all arithmetic and logical operations,
• X and Y, used as counters and for indexing. They can be incremented and decremented.
• S the stack pointer. A fixed block of 256 bytes of memory is used for the stack.

Here is some sample code, for the well known problem of printing 2 hex digits representing a byte initially passed as an argument in the accumulator, A:

BIN2HEX         ; Convert 0..15 in A to Hex digit
        CMP     #0A     ; immediate hex. Compare sets status flags
        BCC     $1      ; Branch less than since 6502 leaves C=0 to indicate borrow
        ADC     #6      ; adds 7 since Carry is set
$1      ADC     #30     ; now C=0, we have ASCII character
        RTS             ; return with it in A

OUTHEX          ; Output byte in A as 2 hex digits (ASCII chars)
        PHA             ; push a copy on stack
        LSR  A          ; Process left nibble
        LSR  A          ; by shifting right 4 bits
        LSR  A
        LSR  A
        JSR     BIN2HEX ; call the above
        JSR     OUTCHAR ; given output routine
        PLA             ; pop original byte from stack
        AND     #0F     ; mask to get right nibble
        JSR     BIN2HEX
        JSR     OUTCHAR
        RTS             ; all done

        LDX     #12     ; print 12 chars
        LDY     #0
LOOP
        LDA     HELLO,Y ; String starts at HELLO, indexed by Y
        JSR     OUTCHAR
        INY
        DEX             ; decrement counter 
        BNE     LOOP    ; and test for 0

80x86

The 4 16 bit "general purpose" registers are named AX, BX, CX, and DX. Each is divided into two 8-bit halves, named AH and AL, BH... etc. so that they can be used as 8 8-bit registers if desired. AX is the accumulator, BX may be used as an indirect address, CX as a counter, and DX for I/O.

4 more 16-bit registers are used primarily to hold addresses. They are named SI, DI, BP, and SP. SP is the stack pointer.

Move, arithmetic, and logical instructions have 2 operands, destination and source. The destination is also the first operand of instructions like ADD. One operand must be a register, the other can be a register, memory, or immediate (source only.) For example:

          ADD   AX, mynumber
          MOV   sum, AX

Here is the byte printed as 2 hex characters example, in 8086 assembly language. Note: this assembler is not case sensitive.
BIN2HEX:                ; Convert 0..15 in AL to Hex digit
        CMP     AL, 0AH ; immediate hex. Compare sets status flags
        JB      numeric ; Branch "below" = less than, unsigned
        ADD     AL, 7   ; adds 7 to skip 7 chars between '9' and 'A'
numeric:
        ADD     al,30h  ; make it ASCII character
        RET             ; return with it in AL

OUTHEX:         ; Output byte in AL as 2 hex digits (ASCII chars)
        PUSH    AX      ; push a copy on stack  (must push 16 bits)
        MOV     CL,4    ; Shift count of 4 bits (must use CL for this)
        SHR     AL,CL   ; Process left nibble
                        ; by shifting right 4 bits
        CALL    BIN2HEX ; call the above
        CALL    OUTCHAR ; given output routine
        POP     AX      ; pop original byte from stack
        AND     AL,0Fh  ; mask to get right nibble
        CALL    BIN2HEX
        CALL    OUTCHAR
        RET             ; all done