Loi phase type dans les réseaux d'automates stochastiques, ID

Les Réseaux d'Automates Stochastiques (SAN en anglais) est un formalisme de haut niveau qui permet la modélisation de chaînes de Markov très grandes et très complexes de façon compacte et structurée. Avec le temps continu, le délai de franchissement des transitions (durée de tir des transitions) dans les SANs suit une distibution exponentielle, ce qui permet de modéliser un ensemble important de systèmes ayant des activités concurrentes.
Cependant, l'emploi de distributions plus générales reste toujours souhaitable pour la modélisation de nombreux phénomènes réels, notamment dans le contexte de la fiabilité. Il s'agit, notament, de la famille de distributions phase-type qui peuvent être décrites par un "graphe de services exponentiels". Elles sont constituées d'une succession d'étapes où la durée de service de l'étape numéro 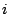$i$ suit une loi exponentielle de moyenne 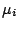$\mu_{i}$. Comme cas particulier de cette famille de distributions, nous citons la distribution d'Erlang, hyper-exponentielle, et Cox qui généralise les deux premiers types de distribution. L'utilisation de la loi Phase-Type a un grand intérêt, car elle permet de décrire de durées réelles et plus complexes que celles pouvant être décrites par la loi exponentielle: par exemple, le processus de fabrication d'un produit peut passer par plusieurs étapes de construction et de vérification, avant que le produit ne soit validé. Les taux de ces différentes étapes suivent des lois exponentielles.
D'autre part, les lois Phase-Type ne sont pas des lois "sans mémoire". Lorsqu'une autre transition est franchie, nous devons déterminer quoi faire avec le travail déjà réalisé par une transition Phase-Type en cours. Cela peut se faire en distinguant les deux politiques de mémoire d'une transition Phase-Type:

Recommencer (Restart): le travail est interrompu, et le temps déjà passé est perdu. Le travail est repris lorsque la transition sera à nouveau franchissable (ce qui peut être immédiatement). Les lois exponentielles "sans mémoire" ont, de part la propriété de la loi, ce type de politique. Pour les lois Phase-Type, ce comportement doit être pris en compte dans la modélisation.

Reprendre (Resume): au contraire de la politique Recommencer, lors du franchissement d'une autre transition, on conserve le temps déjà écoulé. La prochaine fois que la transition sera franchissable (qui peut être une continuation), c'est le temps résiduel qui sera utilisé comme délai de franchissement éventuel.
Notre approche consiste à introduire les transitions phase-type directement au modèle SAN, en décrivant aussi leur sémantique dans le modèle lui-même (qui sera appelé modèle PH-SAN). Lors du calcul, ce modèle PH-SAN est transformé en un modèle SAN standard (avec ses transitions locales, fonctionnelles et synchronisantes), en prenant en considération les différentes politiques d'éxécution de transitions Phase-type. Ensuite, les matrices élémentaires du descripteur (matrice de transition de la chaîne de Markov sous-jacente) sont générées à partir de ce nouveau modèle.