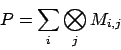Approche Modulaire et Représentation Tensorielle

Les Réseaux d'Automates Stochatiques (RAS) introduits par B. Plateau en 1984 permettent, de simplifier la représentation des chaînes de Markov. En effet, les sytèmes modélisés sont souvent constitués de plusieurs composantes qui évoluent en parallèles et qui se synchronisent sur certains évènements communs. Dans ces cas là, l'espace d'états de la chaîne de Markov global est inclus dans le produit cartésien des espaces d'états de chacune des composantes. La modélisation par les RAS permet de représenter chaque composante en isolation et de spécifier les évènements synchronisants. Par exemple, si l'on cherche à représenter un réseau de files d'attente de taille , la taille de l'espace d'état global est alors que si l'on représente uniquement chacune des composantes, il suffit de représenter $N \times B$ états.

Les transitions de chaque composante de la chaîne sont décrites par un automate dont les sommets sont étiquetés par les valeurs de la composante et dont les arcs portent des marques. C'est à partir de ces automates que l'on construit la chaîne multi-dimensionnelle dont les sommets sont ceux de l'espace produit.

Dans un Réseau d'Automates Stochastiques, chaque automate représente une vue partielle du système à modéliser. Les dépendances entre les automates expriment les contraintes de synchronisation entre ces diverses vues partielles. La version mathématique du problème se pose en termes de relations entre les composantes d'un processus de Markov multidimentionnel à espace d'états fini. Il est défini deux types de dépendances élémentaires : les synchronisations d'un groupe de transitions, et les dépendances fonctionnelles où l'état d'autres automates influence le taux de transition courant d'un automate particulier.

Les arcs de la chaîne globale et les marques portées par ces arcs sont générés grâce à une méthode qui utilise les marques portées par les arcs des automates. Chaque automate est représenté par un ensemble de matrices, dites matrices locales ( $M_{i,j}$ ) et en appliquant des opérateurs de l'algèbre de Kronecker sur ces matrices, on construit automatiquement le générateur ou la matrice de transition de la chaîne globale (voir Eq. 1). A la différence des approches énumératives où l'on doit générer extensivement cette matrice, nous en obtenons une représentation compacte dont le stockage en mémoire est très efficace. Qui plus est, cette représentation est compatibles avec certains algorithmes de résolution et elle laisse paraître des propriétés structurelles de la matrice pour employer des algorithmes ad-hocs.

$\begin{displaymath} P = \sum_i \bigotimes_j M_{i,j} \end{displaymath}$

(1)

Le formalisme mathématique sous-jacent permet des optimisations numériques et se prète à la parallélisation comme l'ont montré nos travaux. Cet aspect est extrêmement important dans le domaine des protocoles où l'explosion du nombre des états est un phénomène critique. La représentation sous forme de produit de Kronecker est valable en temps discret comme en temps continu et permet donc de considérer différents modèles temporels.

Le formalisme des RAS est très proche des méthodes de représentation utilisées dans le domaine de la validation et offre une possibilité réelle d'intégration des approches d'évaluation et de validation. Déjà, les résultat principaux (la forme tensorielle et les algorithmes adaptés) ont été transposés à d'autres formalismes de décomposition :

réseaux de Petri grâce aux travaux de Haddad-Moreaux en France, de Donattelli, Buchholtz et Kemper en Europe, Ciardo aux USA,
Algèbre de Processus basés sur CSP grâce en particulier aux travaux de Hillston-Kloul,
"model checking" stochastique (Travaux de Katoen, ``model checker'' APPN par l'équipe de Buchholtz).

D'autres extensions vers LOTOS ont également été proposées dans la littérature et permettent de faire converger des méthodes qualitatives et quantitatives; si ce n'est vers un formalisme du moins vers des algorithmes reposant sur les mêmes approches à base d'algèbre tensorielle.

Il existe actuellement plusieurs méthodes de résolution pour le problème stationnaire. La première famille consiste à utiliser une optimisation du produit d'un vecteur par un produit tensoriel de matrice. Cette approche est utilisée dans des algorithmes itératifs dont le plus simple est l'algorithme des puissances mais aussi par des algorithmes projectifs tels que l'algorithme d'Arnoldi ou GMRES dont la convergence est beaucoup plus rapide. Ces algorithmes sont implantés dans le logiciel PEPS. Récemment nous avons aussi contribués à la proposition d'une approche itérative d'agrégation/desagrégation reposant sur des propriétés de "lumpabilité" de la chaîne. Cette approche permet de réduire l'espace des états ou de simplifier l'algorithme de résolution. Des conditions suffisantes sur les RAS peuvent être testée avec une complexité liée au nombe d'autoamtes et non pas au nombre des états. Les travaux récents (les notres comme ceux des équipes européennes ou américaines) ont donc montré que la représentation tensorielle permettaient de traiter des problèmes de grande taille, y compris lorsque les approches conventionnelles reposant sur des matrices en format creux ne fonctionnent plus, faute de place en mémoire.

Certaines mesures de sûreté de fonctionnement comme la fiabilité, la disponibilité sur un intervalle de temps fixé ou plus généralement, la performabilité nécessitent une étude approfondie en régime transitoire de la chaîne de Markov modélisant le système et sur laquelle ces mesures sont définies.

Le concept de performabilité a été développé par John Meyer, dans les années 1980, dans le but d'unifier les aspects performance et fiabilité des systèmes informatiques. La notion de performabilité peut être vue comme un raffinement de la disponibilité sur un intervalle. En effet, pour étudier la disponibilité d'un système sur un intervalle, il est nécessaire de classer les états du système en deux classes : la classe des états opérationnels et celle des états non opérationnels. L'étude de la performabilité d'un système requiert un classement plus fin de l'ensemble des états du système. À chaque état du système, on associe un niveau de performance ou taux de récompense $\rho_i \in R^+$ qui donne une mesure de la performance du système lorsqu'il se trouve dans l'état . La mesure de performabilité la plus étudiée est la récompense cumulée par le système sur l'intervalle . Cette variable aléatoire est notée et est définie, pour $t \in R^+$ , par

$\begin{displaymath}Y_t = \int_{0}^{t} \rho_{X_u} du,\end{displaymath}$

où

représente l'état du système à l'instant

. Lorsque les taux de récompense ne prennent que les valeurs

, la variable

est appelée disponibilité sur l'intervalle

De nombreux travaux ont porté sur l'étude de . L'équipe ARMOR a obtenu, à travers les travaux de B. Sericola, plusieurs résultats nouveaux qui ont donné lieu à de nombreux algorithmes permettant le calcul de la distribution de . Ces travaux ont aussi permis de détecter le régime stationnaire du processus. En effet, lorsque l'on étudie un système en régime transitoire, il est important est de savoir si l'instant auquel on s'intéresse n'est pas suffisamment grand pour considérer le système en régime stationnaire. Dans ce cas, cela signifie qu'il existe un instant $T \leq t$ à partir duquel le régime stationnaire est pratiquement atteint. Pour certaines mesures de performabilité, on arrive à détecter cet instant de manière très précise et contrôlée, ce qui permet non seulement d'économiser les calculs de la mesure transitoire entre et , mais aussi d'avoir une évaluation très précise de la mesure stationnaire associée sans la calculer.

Néanmoins, les espaces d'états de grande taille posent bien évidemment de gros problèmes et les algorithmes pour le calcul des mesures transitoires de la sûreté de fonctionnement n'ont pas été étudiés dans le cadre de l'approche tensorielle. Il y a donc là des problèmes algorithmiques nouveaux et la complémentarité entre les trois équipes (ARMOR est spécialiste de ces algorithmes alors que PRiSM et ID sont à l'origine des approches tensorielles) doit nous permettre de les résoudre.