Simulation d'événements rares et simulation parfaite, ID

L'évaluation de la probabilité d'événements rares constitue l'une des difficultés majeures dans le calcul de la disponibilité asymptotique de grands systèmes. Celui-ci est modélisé par une chaîne de Markov multidimensionnelle, la taille de l'espace d'état explose en fonction de la dimension de la chaîne. L'espace d'état est partitionné en 2 : l'ensemble des états de fonctionnement normal ${\cal A}$ et son complémentaire ${\cal A}^c$. L'objectif est alors d'estimer la probabilité stationnaire de la chaîne d'être dans l'ensemble ${\cal A}^c$. Dans les cas pratiques la probabilité stationnaire de ${\cal A}^c$ est très faible. Par conséquent, les méthodes traditionnelles de simulation ne sont pas efficaces car le temps de stabilisation de la chaîne est très long (dépendance de l'état initial) et les échantillons générés sont fortement corrélés.

Une alternative consiste alors à effectuer des simulations dites parfaites, qui, avec un surcoût lié au suivi de plusieurs trajectoires simultanément, échantillonnent directement selon la loi stationnaire de la chaîne. Cette méthode, initiée par Propp & Wilson, simule différentes trajectoire de la chaîne en inversant le temps. Elle est d'autant plus efficace si les fonctions de transition de la chaîne sont monotones.

Dans un premier temps nous représentons la chaîne de Markov par un schéma itératif dirigé par des événements

$$X_{n+1}=\Phi(X_{n},e_{n+1}).$$

En utilisant des propriétés de monotonie de la fonction 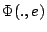$\Phi(.,e)$ pour tout événement 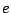$e$, nous construisons un noyau de simulation parfaite permettant l'échantillonnage de la chaîne. De plus, les ensembles ${\cal A}^c$ étant croissants il est possible d'interrompre la simulation avant le couplage global des trajectoires analysées en parallèle et donc d'accélérer la simulation. Les principaux résultats obtenus sont :

Modélisation

Les systèmes à base de réseaux markoviens de files d'attente possèdent des propriétés de monotonie. En particulier les politiques de routage dans les systèmes à capacité finie (rejet, blocage, débordement,..) sont monotones.

Discrétisation

La représentation du système par des événements dirigés par des processus de Poisson indépendants permet une uniformisation du processus (passage en temps discret) préservant les propriétés de monotonie.

Accélération

L'estimation de la probabilité d'être dans un ensemble croissant a été accélérée par des fonctions d'arrêt adaptées.

Les résultats obtenus ont été implantés dans un logiciel de simulation 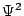$\Psi^2$. A partir d'une description du système sous forme d'un ensemble d'événements et d'une fonction de ``reward'' monotone (appartenance à ${\cal A}^c$), il fournit un échantillon distribué selon la probabilité stationnaire d'être dans ${\cal A}^c$.

Cet environnement a été testé sur des exemples caractéristiques : rejet dans les systèmes à routage par débordement avec l'estimation de la probabilité de saturation; analyse du blocage dans des lignes de production; saturation dans des réseaux d'interconnection...

Par exemple pour un réseau d'interconnection de type delta comportant 32 files de capacité 30, la taille de l'espace d'état est de 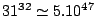$31^{32}\simeq 5.10^{47}$, le temps de génération d'une valeur d'un échantillon permettant l'estimation de la loi marginale d'une file au dernier étage est de l'ordre de $100\mu s$ (sur un PC linux 1.2GHz, 512Mo). 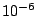L'utilisation d'une telle méthode permet alors, en force brute, de simuler des échantillos significatifs pour l'estimation de probabilités faibles (de l'ordre de $10^{-6}$ en 3 heures sur un PC standard).

Ce travail doit être approfondi sur plusieurs points :

Méthodologie

Cette approche doit être combinée à d'autres techniques, en particulier les méthodes de réduction de variance (variables antithétiques, Importance sampling,...)

Modélisation

Actuellement seuls certains types d'événements monotones ont été implantés, les disciplines de routages telles que ``Join the shortest queue'', décomposition de clients, les arrivées groupées, certain types de clients négatifs présentent également des propriétés de monotonie et doivent donc être implémentées et testées. De plus d'autres événements tels que la fusion de clients , les départs groupés,... sont ``anti-monotones''. Cette propriété doit être explorée plus en détail.

Expérimentation

Les exemples utilisés attaquent des problèmes basés sur les réseaux de files d'attente. Peut-on généraliser cette approche à d'autres formalismes tels que les réseaux d'automates stochastiques ? Intuitivement, la réponse devrait être positive, il faudrait alors combiner les approches de bornes stochastiques (cf sections précédentes) avec la simulation parfaite.