Une autre approche qui a fait l'objet de travaux préliminaires au PRiSM
utilise les propriétés du dyoide ![]() .
L'idée est ici de concevoir une nouvelle définition constructive de
la distribution de
probabilités stationnaires d'une chaine de Markov en temps discret en
utilisant les opérateurs
.
L'idée est ici de concevoir une nouvelle définition constructive de
la distribution de
probabilités stationnaires d'une chaine de Markov en temps discret en
utilisant les opérateurs ![]() et
et ![]() puis
d'en dériver des encadrements.
puis
d'en dériver des encadrements.
La construction que nous avons établie définit la distribution
stationnaire ![]() comme limite supérieure d'un schéma iteratif croissant
sur des vecteurs à composantes positives. On n'utilise donc pas ici de
probabilités mais des matrices positives et des vecteurs positifs.
Ce schéma utilise les opérateurs
comme limite supérieure d'un schéma iteratif croissant
sur des vecteurs à composantes positives. On n'utilise donc pas ici de
probabilités mais des matrices positives et des vecteurs positifs.
Ce schéma utilise les opérateurs ![]() ,
, ![]() et la multiplication
par des scalaires positifs. De même un schéma itératif
décroissant utilisant les opérateurs
et la multiplication
par des scalaires positifs. De même un schéma itératif
décroissant utilisant les opérateurs ![]() et
et ![]() a été
démontré.
Le schémà croissant repose sur les idées suivantes:
a été
démontré.
Le schémà croissant repose sur les idées suivantes:
- Supposons que nous ayons construit un vecteur positif
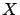 dont toutes les
composantes sont inférieures à celle de
dont toutes les
composantes sont inférieures à celle de 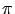 .
Alors, puisque
.
Alors, puisque 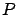 est une matrice positive,
est une matrice positive, 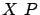 est un vecteur inférieur à
est un vecteur inférieur à 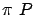 , c'est à dire
, c'est à dire 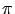 . Donc
. Donc 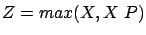 est, composante par
composante, entre
est, composante par
composante, entre 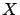 et
et 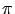 .
.
- l'inégalité triviale suivante donne le point initial pour la
séquence:
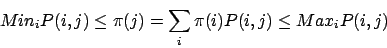
Posons alors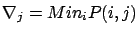 . La seconde partie de
l'inégalité permet l'initialisation de la séquence décroissante
des bornes supérieures.
. La seconde partie de
l'inégalité permet l'initialisation de la séquence décroissante
des bornes supérieures.
- Le schéma initial a de multiples limites.
On le modifie donc pour que le seul point limite soit la distribution
stationnaire
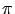 .
.
Nous n'avons, pour le moment, de preuve de l'algorithme que lorsque
![]() est non nul, mais des expériences
numériques montrent que, même dans le
cas contraire, on peut faire converger la séquence par un choix
judicieux du vecteur initial.
Un point important est que, dans cette
nouvelle approche, on obtient à chaque étape
une borne pour toutes les composantes
de la distribution. La qualité du résultat va donc s'accroitre
avec le temps de calcul.
est non nul, mais des expériences
numériques montrent que, même dans le
cas contraire, on peut faire converger la séquence par un choix
judicieux du vecteur initial.
Un point important est que, dans cette
nouvelle approche, on obtient à chaque étape
une borne pour toutes les composantes
de la distribution. La qualité du résultat va donc s'accroitre
avec le temps de calcul.
Le projet se propose de prouver d'autres bornes associées à des
simplification de calcul. Par exemple,
dans le calcul de la borne, il est possible de remplacer
certains éléments de ![]() (positifs par définition)
par des valeurs nulles, tout en conservant
le vecteur
(positifs par définition)
par des valeurs nulles, tout en conservant
le vecteur ![]() . Clairement, le calcul de la borne est plus simple
car il y a maintenant moins d'éléments non nuls et forunit une
borne (car on a élmininé des termes positifs de la somme). De même on peut
annuler des colonnes entières de
. Clairement, le calcul de la borne est plus simple
car il y a maintenant moins d'éléments non nuls et forunit une
borne (car on a élmininé des termes positifs de la somme). De même on peut
annuler des colonnes entières de ![]() pour pouvoir traiter le cas de
matrices infinies. La preuve de la borne repose sur des propriétés
des opérateurs
pour pouvoir traiter le cas de
matrices infinies. La preuve de la borne repose sur des propriétés
des opérateurs ![]() et
et ![]() et de la multiplication par des variables
positives.
et de la multiplication par des variables
positives.
Au cours du projet, ces algorithmes seront implantés dans PEPS. Certains fonctionnent déjà sur la représentation tensorielle puisqu'ils emploient le produit vecteur-matrice, qui a été longuement étudié dans l'approche tensorielle. Par contre, la simplification d'un réseau d'automate pour minimiser le calcul est encore un problème ouvert.