Perfect Simulation

The perfect simulation [Wil96], derived from the algorithm of Coupling from the past, designed by Propp & Wilson (1996), gives a method to directly generate a sample according to the stationary distribution of Markov chains.
The scheme of this algorithm is to consider all possible initial values and observe their trajectories.
But to obtain an exact sample, we must run the simulation from a distant point in the past up until the present. The stopping criteria of the simulation is therefore the coalesce time of different trajectories at time 0.

$$\mathbf{P}= \left(\begin{array}{ccc} \frac{1}{2} & \frac{1}{2} & 0 \\ 0 & 0 & 1 \\ \frac{1}{2} & 0 & \frac{1}{2} \\ \end{array} \right)$$

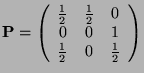
In use, for example, the inverse of pdf, apply to each transition probability $p(x,.)$, we obtain a (non-unique) representation of the chain:

For $x=0,2$,

$$\Phi(x,u)= \left\{\begin{array}{cc} 0 & \textrm{si $u\leq \frac 1 2$.} \\ min_x({x+1,2}) & \textrm{sinon.} \end{array} \right.$$

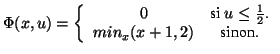
and

$$\Phi(1,u)=2.$$

Figure 1.7: Coupling after 4 iterations.